某汽车租赁公司拥有20辆汽车。据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元。设公司每日租出x辆车时,日收益为y元。(日收益=日租金收入-平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
相关知识点
推荐套卷
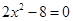
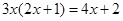 .
. 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
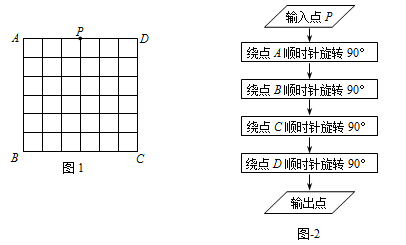
 ,0)时,求此时DP的长及点D的坐标。
,0)时,求此时DP的长及点D的坐标。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号