设Sn为数列{an}为前n项和，对任意的
都有
（m为常数且m>0）
（1）求证：{an}为等比数列；
（2）设数列{an}的公比q=f(m)，数列{bn}满足
，求数列{bn}的通项公式；
（3）在（2）的条件下，求数列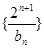
的前n项和Tn。
相关试题
的值；（2）若
的值。
图象的对称中心的横坐标；
，求函数
的定义域为集合A,函数
的定义域为集合B.
A，求实数
的取值范围。
（
）.
的单调区间；
在
内有且只有一个极值点, 求a的取值范围.
，一个焦点是F（0，1）．
过点F交椭圆于A、B两点，且
，求直线推荐套卷
设Sn为数列{an}为前n项和，对任意的都有（m为常数且m>0）
（1）求证：{an}为等比数列；
（2）设数列{an}的公比q=f(m)，数列{bn}满足，求数列{bn}的通项公式；
（3）在（2）的条件下，求数列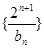的前n项和Tn。
粤公网安备 44130202000953号