在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF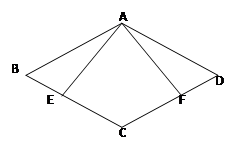
(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
相关知识点
推荐套卷
在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF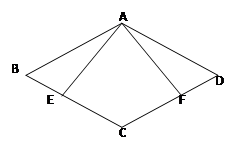
(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。