（本小题满分12分）
如图，在平面直角坐标系xOy中，平行于x轴且过点A(3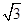
，2)的入射光线 l1
被直线l：y=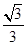
x反射．反射光线l2交y轴于B点，圆C过点A且与l1, l2都相切.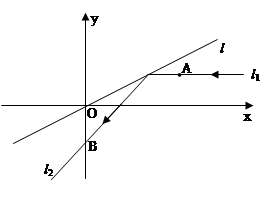
(1)求l2所在直线的方程和圆C的方程；
(2)设
分别是直线l和圆C上的动点，求
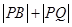的最小值及此时点
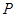的坐标．
中，
所对的边分别为
，
，
．
；
，求
，已知
，求角A，B，C的大小。
的长度的最大值；
，且
，求
的值。
与
互相垂直，其中
．
和
的值；
，求
的值．
的定义域是
，求实数
的取值范围。推荐套卷
（本小题满分12分）
如图，在平面直角坐标系xOy中，平行于x轴且过点A(3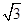，2)的入射光线 l1
被直线l：y=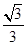x反射．反射光线l2交y轴于B点，圆C过点A且与l1, l2都相切.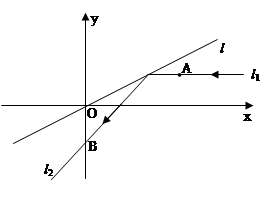
(1)求l2所在直线的方程和圆C的方程；
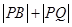(2)设分别是直线l和圆C上的动点，求的最小值及此时点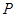的坐标．
粤公网安备 44130202000953号