(本小题满分13分)已知函数 (其中
(其中 且
且 为常数)的图像经过点A
为常数)的图像经过点A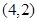 、B
、B .
. 是函数
是函数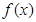 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求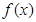 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前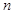 项和为
项和为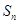 ,证明:
,证明: 。
。
推荐套卷
(本小题满分13分)已知函数 (其中
(其中 且
且 为常数)的图像经过点A
为常数)的图像经过点A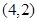 、B
、B .
. 是函数
是函数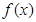 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求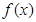 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前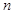 项和为
项和为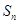 ,证明:
,证明: 。
。