如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以D为圆心似长为半径作
圆O、C为半圆AB上不与A、B重合的一动点，射线AC交⊙O于点E，BC=a，AC=b，
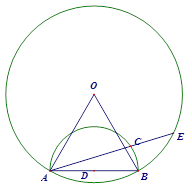
（1）求证：AE=b+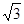
a；
（2）求a+b的最大值；
（3）若m是关于x的方程：x+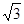ax=b+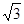ab的一个根，求m的取值范围．
相关试题
以下正确的是（）
，
、
时，一次函数的函数值y满足
，则一次函数的解析式为
或
和
相交于x轴上一点，则
的值是
的图像上有两点A（a、3）和B（3、b），则
的值（）
；
．
相关知识点
推荐套卷
如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以D为圆心似长为半径作
圆O、C为半圆AB上不与A、B重合的一动点，射线AC交⊙O于点E，BC=a，AC=b，
（1）求证：AE=b+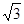a；
（2）求a+b的最大值；
（3）若m是关于x的方程：x+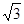ax=b+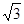ab的一个根，求m的取值范围．
粤公网安备 44130202000953号