(本小题满分12分)
如图椭圆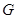 :
:
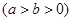 的两个焦点为
的两个焦点为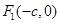 、
、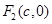 和顶点
和顶点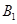 、
、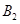 构成面积为32的正方形.
构成面积为32的正方形.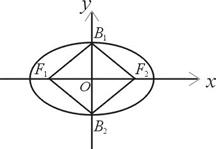
(1)求此时椭圆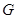 的方程;
的方程;
(2)设斜率为 的直线
的直线 与椭圆
与椭圆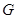 相交于不同的两点
相交于不同的两点 、
、 、
、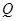 为
为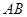 的中点,且
的中点,且 . 问:
. 问: 、
、 两点能否关于直线
两点能否关于直线 对称. 若能,求出
对称. 若能,求出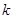 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
推荐套卷
(本小题满分12分)
如图椭圆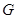 :
:
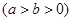 的两个焦点为
的两个焦点为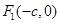 、
、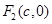 和顶点
和顶点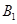 、
、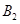 构成面积为32的正方形.
构成面积为32的正方形.
(1)求此时椭圆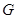 的方程;
的方程;
(2)设斜率为 的直线
的直线 与椭圆
与椭圆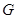 相交于不同的两点
相交于不同的两点 、
、 、
、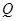 为
为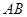 的中点,且
的中点,且 . 问:
. 问: 、
、 两点能否关于直线
两点能否关于直线 对称. 若能,求出
对称. 若能,求出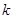 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.