如图，已知抛物线C1： y=x2, 与圆C2： x2+(y+1)2="1," 过y轴上一点A（0, a）（a>0）作圆C2的切线AD，切点为D（x0, y0）.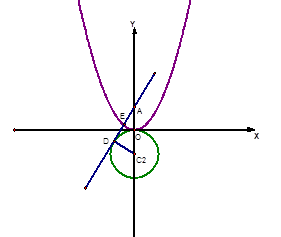
（1）证明：(a+1)(y0+1)=1
（2）若切线AD交抛物线C1于E，且E为AD的中点，求点A纵坐标a.
是
的极值点，求
上的最小值和最大值；
上是增函数，求实数
的取值范围
与
；
的反函数
及
上是增函数
推荐套卷
如图，已知抛物线C1： y=x2, 与圆C2： x2+(y+1)2="1," 过y轴上一点A（0, a）（a>0）作圆C2的切线AD，切点为D（x0, y0）.
（1）证明：(a+1)(y0+1)=1
（2）若切线AD交抛物线C1于E，且E为AD的中点，求点A纵坐标a.
粤公网安备 44130202000953号