（本小题12分）已知：以点C (t,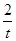 
)(t∈R , t ≠ 0)为圆心的圆与
轴交于点O, A，
与y轴交于点O, B，其中O为原点．
(1）求证：△OAB的面积为定值；
(2）设直线y = –2x+4与圆C交于点M, N，若
，求圆C的方程．
求证：
，
在点（1，f（1））处的切线为
，若
相切，求a的值；
在
上是增函数，求a的取值范围．
，其中
为正整数．
，
，
的值；
的正整数
，且
,
,试证：
。相关知识点
推荐套卷
（本小题12分）已知：以点C (t, 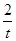)(t∈R , t ≠ 0)为圆心的圆与轴交于点O, A，
与y轴交于点O, B，其中O为原点．
(1）求证：△OAB的面积为定值；
(2）设直线y = –2x+4与圆C交于点M, N，若，求圆C的方程．
粤公网安备 44130202000953号