已知,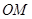 、
、 分别是
分别是 ,
, 的角平分线.
的角平分线.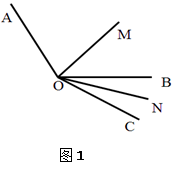

(1)如图1,若 ,
, ,则
,则  ;
;
(2)如图1,若 ,
,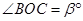 ,能否求出
,能否求出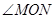 的度数?若能,求出其值,若不能,试说明理由;
的度数?若能,求出其值,若不能,试说明理由;
(3) 如图2,若 ,
,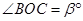 ,是否仍然能求出∠MON的度数,若能,求
,是否仍然能求出∠MON的度数,若能,求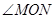 的度数(用含
的度数(用含 或
或 的式子表示),并从你的求解过程中总结出你发现的规律 .
的式子表示),并从你的求解过程中总结出你发现的规律 .
已知,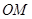 、
、 分别是
分别是 ,
, 的角平分线.
的角平分线.

(1)如图1,若 ,
, ,则
,则  ;
;
(2)如图1,若 ,
,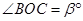 ,能否求出
,能否求出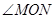 的度数?若能,求出其值,若不能,试说明理由;
的度数?若能,求出其值,若不能,试说明理由;
(3) 如图2,若 ,
,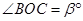 ,是否仍然能求出∠MON的度数,若能,求
,是否仍然能求出∠MON的度数,若能,求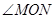 的度数(用含
的度数(用含 或
或 的式子表示),并从你的求解过程中总结出你发现的规律 .
的式子表示),并从你的求解过程中总结出你发现的规律 .