(本小题12分) 正项数列{an}满足a1=2，点An（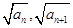
）在双曲线y2-x2=1上，点（
）在直线y=-
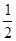x+1上，其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式；
②设Cn=anbn，证明 Cn+1＜Cn
③若m-7anbn＞0恒成立，求正整数m的最小值。
为两个互相垂直的单位向量，求
是两个垂直的单位向量，且
（２）若
的值。
满足
求
夹角为
， 
的值。
推荐套卷
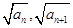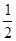(本小题12分) 正项数列{an}满足a1=2，点An（）在双曲线y2-x2=1上，点（）在直线y=-x+1上，其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式；
②设Cn=anbn，证明 Cn+1＜Cn
③若m-7anbn＞0恒成立，求正整数m的最小值。
粤公网安备 44130202000953号