某市旅游部门开发一种旅游纪念品，每件产品的成本是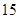
元，销售价是
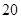元，月平均销售
件．通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为
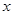
，那么月平均销售量减少的百分率为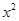
．记改进工艺后，旅游部门销售该纪念品的月平均利润是
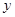（元）．
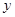（1）写出与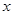的函数关系式；
（2）改进工艺后，确定该纪念品的售价，使旅游部门销售该纪念品的月平均利润最大．
相关试题
中，平面
平面
，
，
，
，
.
平面
；
的大小.
的正三棱锥
，其表面展开图是三角形
，如图. 求
的各边长及此三棱锥的体积
.
中，
为矩形，平面
平面
问
为何值时，四棱锥
与平面
夹角的余弦值.推荐套卷
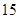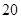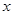
某市旅游部门开发一种旅游纪念品，每件产品的成本是元，销售价是元，月平均销售 件．通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为，那么月平均销售量减少的百分率为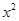．记改进工艺后，旅游部门销售该纪念品的月平均利润是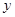（元）．
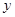（1）写出与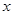的函数关系式；
（2）改进工艺后，确定该纪念品的售价，使旅游部门销售该纪念品的月平均利润最大．
粤公网安备 44130202000953号