（本小题12分）已知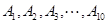
等10所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为
.
（Ⅰ）如果该同学10所高校的考试都参加，试求恰有2所通过的概率；
（Ⅱ）假设该同学参加每所高校考试所需的费用均为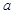
元，该同学决定按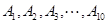顺序参加考试，一旦通过某所高校的考试，就不再参加其它高校的考试，试求该同学参加考试所需费用
的分布列及数学期望.
，
，
,求
的取值范围。
，试用列举法表示集合
。
是双曲线
的两个焦点，点
在双曲线上，且
，
的面积。
变化时，曲线
怎样变化？
，
、
是椭圆上的两点，线段
的垂直
轴相交于点
.证明：
推荐套卷
（本小题12分）已知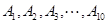等10所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为.
（Ⅰ）如果该同学10所高校的考试都参加，试求恰有2所通过的概率；
（Ⅱ）假设该同学参加每所高校考试所需的费用均为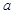元，该同学决定按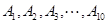顺序参加考试，一旦通过某所高校的考试，就不再参加其它高校的考试，试求该同学参加考试所需费用的分布列及数学期望.
粤公网安备 44130202000953号