(本小题满分10分)
已知圆O: ,圆C:
,圆C: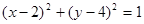 ,由两圆外一点
,由两圆外一点 引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.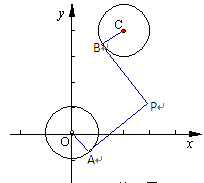
(Ⅰ)求实数a、b间满足的等量关系;
(Ⅱ)求切线长|PA|的最小值;
(Ⅲ)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
推荐套卷
(本小题满分10分)
已知圆O: ,圆C:
,圆C: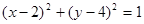 ,由两圆外一点
,由两圆外一点 引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
(Ⅰ)求实数a、b间满足的等量关系;
(Ⅱ)求切线长|PA|的最小值;
(Ⅲ)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.