对n∈N∗不等式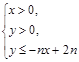
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),⋯,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2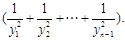
证明:当n≥2时,
;
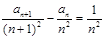(3)在(2)的条件下,试比较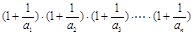
与4的大小关系.
推荐套卷
对n∈N∗不等式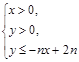所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),⋯,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2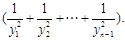证明:当n≥2时,;
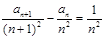(3)在(2)的条件下,试比较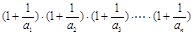与4的大小关系.
粤公网安备 44130202000953号