如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.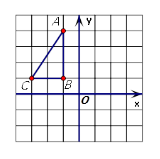
(1)作出△ABC关于y轴对称的△A’B’C’;
(2)若点D在图中所给的网格中的格点上,且以A、B、C、D为顶点的四边形为平行四边形,请直接写出点D的坐标.
相关知识点
推荐套卷
如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.
(1)作出△ABC关于y轴对称的△A’B’C’;
(2)若点D在图中所给的网格中的格点上,且以A、B、C、D为顶点的四边形为平行四边形,请直接写出点D的坐标.