（本小题满分14分）已知函数
处取得极值2。
(Ⅰ)
求函数
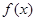的表达式；
（Ⅱ）当
满足什么条件时，函数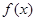在区间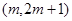
上单调递增？
（Ⅲ）若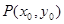
为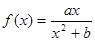
图象上任意一点，直线与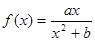的图象切于点P，求直线的斜率
的取值范围
相关试题
的不等式
的解集为
，不等式
的解集为
．
，求
，求正数
的取值.
，其中实数
.
时，求不等式
的解集；
的解集为
，求
的值.
时，解不等式
；
恒成立，求实数
的取值范围
的解集；
的不等式
在
上无解，求实数
的取值范围
.
的解集为
，求
的值；
，使
，求相关知识点
推荐套卷
（本小题满分14分）已知函数处取得极值2。
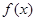(Ⅰ)求函数的表达式；
（Ⅱ）当满足什么条件时，函数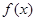在区间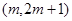上单调递增？
（Ⅲ）若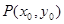为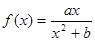图象上任意一点，直线与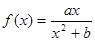的图象切于点P，求直线的斜率的取值范围
粤公网安备 44130202000953号