（本小题满分14分）
如图，在四面体PABC中，PA=PB，CA=CB，D、E、F、G分别是PA，AC、CB、BP的中点．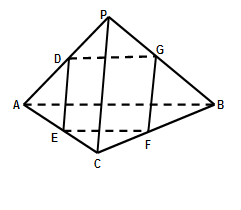
(1)求证：D、E、F、G四点共面；
(2)求证：PC⊥AB；
(3)若△ABC和△PAB都是等腰直角三角形，且AB=2，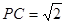
，求四面体PABC的体积．
相关试题
，求
。
的定义域为
，求下列函数的定义域：
； （2）y＝
。
且
。
的值；
和g[
的解析式。相关知识点
推荐套卷
（本小题满分14分）
如图，在四面体PABC中，PA=PB，CA=CB，D、E、F、G分别是PA，AC、CB、BP的中点．
(1)求证：D、E、F、G四点共面；
(2)求证：PC⊥AB；
(3)若△ABC和△PAB都是等腰直角三角形，且AB=2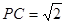，，求四面体PABC的体积．
粤公网安备 44130202000953号