（本小题满分12分）
如果两个椭圆的离心率相等，那么就称这两个椭圆相似.已知椭圆
与椭圆
相似，且椭圆的一个短轴端点是抛物线
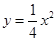的焦点.
（Ⅰ）试求椭圆的标准方程；
（Ⅱ）设椭圆
的中心在原点，对称轴在坐标轴上，直线
与椭圆交于
两点，且与椭圆交于
两点.若线段
与线段
的中点重合，试判断椭圆与椭圆是否为相似椭圆？并证明你的判断.
，
与
的夹角为θ1， 
与
的值.
，且
的最大值。
，比较
与
的大小。推荐套卷
（本小题满分12分）
如果两个椭圆的离心率相等，那么就称这两个椭圆相似.已知椭圆与椭圆相似，且椭圆的一个短轴端点是抛物线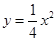的焦点.
（Ⅰ）试求椭圆的标准方程；
（Ⅱ）设椭圆的中心在原点，对称轴在坐标轴上，直线与椭圆交于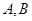两点，且与椭圆交于两点.若线段与线段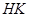的中点重合，试判断椭圆与椭圆是否为相似椭圆？并证明你的判断.
粤公网安备 44130202000953号