如图1，在正方形ABCD中，等腰三角形AEF的顶点E，F分别在BC和CD上.
（1）求证：BE=DF；
（2）若等腰三角形AEF的腰AE比正方形ABCD的边AB长1，BE=5，求正方形ABCD的面积；
（3）若∠EAF=50°，则
①如图1，∠BAE= °；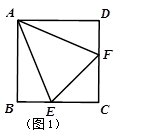
②如图2，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，求∠BAE的大小．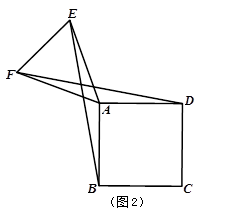
，并将它的解集在数轴上表示出来．
，其中x=﹣3．
，其中
．
，其中
是方程
的根．
，其中
．相关知识点
推荐套卷
如图1，在正方形ABCD中，等腰三角形AEF的顶点E，F分别在BC和CD上.
（1）求证：BE=DF；
（2）若等腰三角形AEF的腰AE比正方形ABCD的边AB长1，BE=5，求正方形ABCD的面积；
（3）若∠EAF=50°，则
①如图1，∠BAE= °；
②如图2，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，求∠BAE的大小．
粤公网安备 44130202000953号