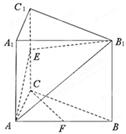
如图,已知直三棱柱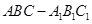 ,
, ,
, 是棱
是棱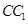 上动点,
上动点, 是
是 中点 ,
中点 , ,
,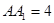 .
.
(1)求证: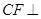 平面
平面 ;
;
(2)当 是棱
是棱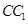 中点时,求证:
中点时,求证: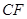 ∥平面
∥平面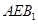 ;
;
(3)在棱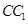 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的大小是
的大小是 ,若存在,求
,若存在,求 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
推荐套卷
如图,已知直三棱柱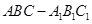 ,
, ,
, 是棱
是棱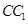 上动点,
上动点, 是
是 中点 ,
中点 , ,
,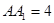 .
.
(1)求证: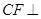 平面
平面 ;
;
(2)当 是棱
是棱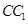 中点时,求证:
中点时,求证: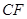 ∥平面
∥平面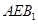 ;
;
(3)在棱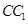 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的大小是
的大小是 ,若存在,求
,若存在,求 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.