（本小题满分14分）
如图，四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90 ，且BC=2AD=2，AB=4，SA=3.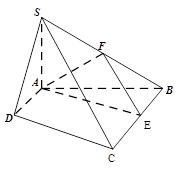
（1）求证：平面SBC⊥平面SAB；
（2）若E、F分别为线段BC、SB上的一点（端点除外），满足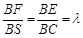
.（
）
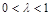①求证：对于任意的
，恒有SC∥平面AEF；
②是否存在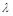
，使得△AEF为直角三角形，若存在，求出所有符合条件的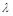值；若不存在，说明理由.
的定义域、周期和单调区间
，求
的值
)=
, 若
2）=1；
的值；（3）解不等式
在
上是减函数；推荐套卷
（本小题满分14分）
如图，四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90 ，且BC=2AD=2，AB=4，SA=3.
（1）求证：平面SBC⊥平面SAB；
（2）若E、F分别为线段BC、SB上的一点（端点除外），满足.（）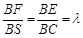
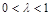①求证：对于任意的，恒有SC∥平面AEF；
②是否存在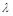，使得△AEF为直角三角形，若存在，求出所有符合条件的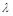值；若不存在，说明理由.
粤公网安备 44130202000953号