已知定义在区间[-p，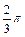
]上的函数y=f(x)的图象关于直线x=－
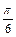对称，当x
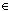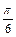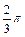[－，]时，函数f(x)=Asin(wx+j)(A>0, w>0,－
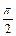<j<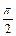)，其图象如图所示。
(1)求函数y=f(x)在[－p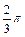，]的表达式；
(2)求方程f(x)=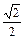
的解。
相关试题
．
的单调性，并证明你的结论；
的
的取值范围．
（
，且
）．
的反函数
的解析式；
．
，
（
，且
）．
的定义域；
的图象关于
轴对称，且与
轴，
的解集．
，
，是否存在实数
，使
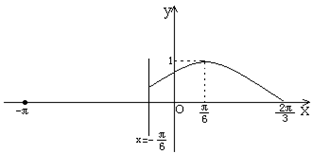
?若存在，求实数相关知识点
推荐套卷
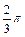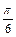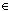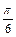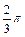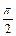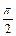已知定义在区间[-p，]上的函数y=f(x)的图象关于直线x=－对称，当x [－，]时，函数f(x)=Asin(wx+j)(A>0, w>0,－<j<)，其图象如图所示。
(1)求函数y=f(x)在[－p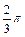，]的表达式；
(2)求方程f(x)=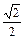的解。
粤公网安备 44130202000953号