（本小题满分12分）
下列三个图中，左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.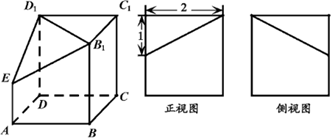
（1）请在正视图的下方，按照画三视图的要求画出该多面体的俯视图（不要求叙述作图过程）；
（2）求该多面体的体积（尺寸如图）.
相关试题
为数列
的前
项和，
，
.
，使得不等式
对任意不小于
为数列
的前
项和，
，
的值；
是等差数列.
中，
.
满足
，设
，且
，求
的值.
为数列
的前
项和，
；数列
满足：
，
，其前
项和为
为数列
的前
，求使不等式
对
都成立的最大正整数
的值.
为等差数列
的前
项和，
.
是等差数列.相关知识点
推荐套卷
（本小题满分12分）
下列三个图中，左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.
（1）请在正视图的下方，按照画三视图的要求画出该多面体的俯视图（不要求叙述作图过程）；
（2）求该多面体的体积（尺寸如图）.
粤公网安备 44130202000953号