如图，转盘被平均分成三块扇形，转动转盘，转动过程中，指针保持不动，转盘停止后，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．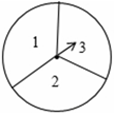
（1）转动转盘一次，转到数字是3的区域的概率是多少？
（2）转动转盘两次，用画树状图或列表的方法求两次指针所指区域数字不同的概率；
（3）在第（2）题中，两次转到的区域的数字作为两条线段的长度，如果第三条线段的长度为5，求这三条线段能构成三角形的概率．
相关试题
的二元一次方程组
的解满足
，求
的取值范围。
，然后选取一个使原式有意义的
的值代入求值。
2）
4）
2）
3） 
4）
的图象与该二次函数的图象交于
点(8,8)，直线与
轴的交点为C，与y轴的交点为B．
为线段
上的一个动点（点
不重合），过
，点
相似？若存在，请求出相关知识点
推荐套卷
粤公网安备 44130202000953号