如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即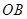 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为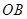 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为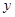 ,
,
(1)设∠CA1O =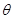 (rad),将y表示成
(rad),将y表示成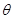 的函数关系式;
的函数关系式;
(2)请你设计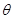 ,当角
,当角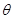 正弦值的大小是多少时,细绳总长
正弦值的大小是多少时,细绳总长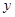 最小,并指明此时 BC应为多长。
最小,并指明此时 BC应为多长。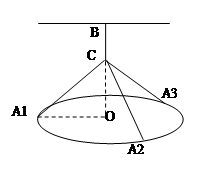
推荐套卷
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即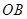 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为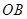 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为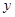 ,
,
(1)设∠CA1O =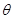 (rad),将y表示成
(rad),将y表示成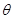 的函数关系式;
的函数关系式;
(2)请你设计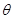 ,当角
,当角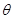 正弦值的大小是多少时,细绳总长
正弦值的大小是多少时,细绳总长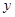 最小,并指明此时 BC应为多长。
最小,并指明此时 BC应为多长。