(本小题满分10分)已知中心在原点O,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为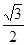 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为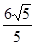 。
。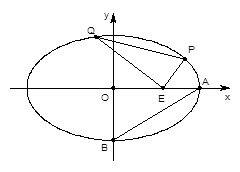
(1)求椭圆C的标准方程;
(2)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,
求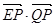 的取值范围.
的取值范围.
推荐套卷
(本小题满分10分)已知中心在原点O,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为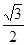 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为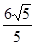 。
。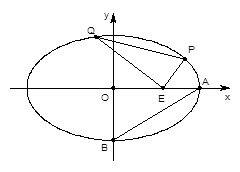
(1)求椭圆C的标准方程;
(2)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,
求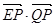 的取值范围.
的取值范围.