已知抛物线 过点
过点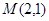 .
.
(I)求抛物线的方程;
(II)已知圆心在 轴上的圆
轴上的圆 过点
过点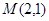 ,且圆
,且圆 在点
在点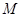 的切线恰是抛物线在点
的切线恰是抛物线在点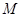 的切线,求圆
的切线,求圆 的方程;
的方程;
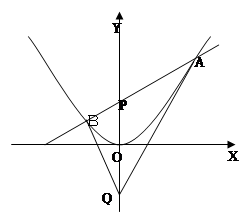
(Ⅲ)如图,点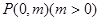 为
为 轴上一点,点
轴上一点,点 是点
是点 关于原点的对称点,过点
关于原点的对称点,过点 作一条直线与抛物线交于
作一条直线与抛物线交于 两点,若
两点,若 ,证明:
,证明: .
.
推荐套卷
已知抛物线 过点
过点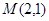 .
.
(I)求抛物线的方程;
(II)已知圆心在 轴上的圆
轴上的圆 过点
过点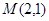 ,且圆
,且圆 在点
在点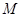 的切线恰是抛物线在点
的切线恰是抛物线在点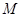 的切线,求圆
的切线,求圆 的方程;
的方程;
(Ⅲ)如图,点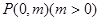 为
为 轴上一点,点
轴上一点,点 是点
是点 关于原点的对称点,过点
关于原点的对称点,过点 作一条直线与抛物线交于
作一条直线与抛物线交于 两点,若
两点,若 ,证明:
,证明: .
.