已知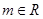 ,命题
,命题 :对任意
:对任意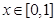 ,不等式
,不等式 恒成立;命题
恒成立;命题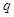 :存在
:存在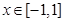 ,使得
,使得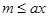 成立
成立
(Ⅰ)若 为真命题,求
为真命题,求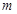 的取值范围;
的取值范围;
(Ⅱ)当 ,若
,若 且
且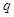 为假,
为假, 或
或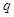 为真,求
为真,求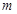 的取值范围。
的取值范围。
(Ⅲ)若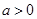 且
且 是
是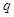 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
相关知识点
推荐套卷
已知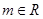 ,命题
,命题 :对任意
:对任意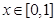 ,不等式
,不等式 恒成立;命题
恒成立;命题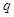 :存在
:存在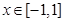 ,使得
,使得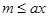 成立
成立
(Ⅰ)若 为真命题,求
为真命题,求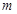 的取值范围;
的取值范围;
(Ⅱ)当 ,若
,若 且
且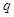 为假,
为假, 或
或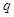 为真,求
为真,求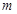 的取值范围。
的取值范围。
(Ⅲ)若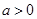 且
且 是
是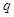 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。