在育民中学举办的“艺术节”活动中,八·二班学生成绩十分突出,小刚将全班获奖作品情况绘成如图的条形统计图(成绩为60分以上的都是获奖作品)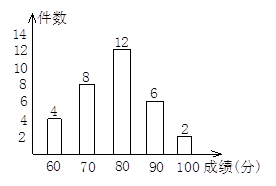
(1)请根据图表计算出八·二班学生有多少件作品获奖?
(2)用计算器求出八·二班获奖作品的平均成绩.
(3)求出这次活动中获奖作品成绩的众数和中位数.
在育民中学举办的“艺术节”活动中,八·二班学生成绩十分突出,小刚将全班获奖作品情况绘成如图的条形统计图(成绩为60分以上的都是获奖作品)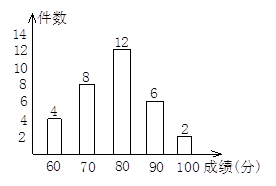
(1)请根据图表计算出八·二班学生有多少件作品获奖?
(2)用计算器求出八·二班获奖作品的平均成绩.
(3)求出这次活动中获奖作品成绩的众数和中位数.
在数轴上的位置如图所示，化简
.
，求此函数的解析式。
,其中
.
，求
的值
为实数，且
，求
的值.
，求下列各式的值：
（2）
粤公网安备 44130202000953号