在平面直角坐标系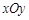 中,对于任意两点
中,对于任意两点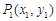 与
与 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若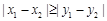 ,则点
,则点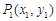 与点
与点 的非常距离为
的非常距离为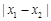 ;
;
若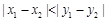 ,则点
,则点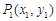 与点
与点 的非常距离为
的非常距离为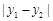 ;
;
例如:点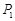 (1,2),点
(1,2),点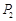 (3,5),因为
(3,5),因为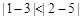 ,所以点
,所以点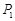 与点
与点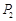 的“非常距离”为
的“非常距离”为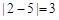 ,也就是图1中线段
,也就是图1中线段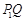 与线段
与线段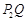 长度的较大值(点Q为垂直于y轴的直线
长度的较大值(点Q为垂直于y轴的直线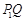 与垂直于x轴的直线
与垂直于x轴的直线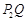 的交点).
的交点).
(1)已知点A(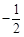 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值.
(2)已知C是直线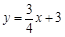 上的一个动点,
上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应点E和点C的坐标.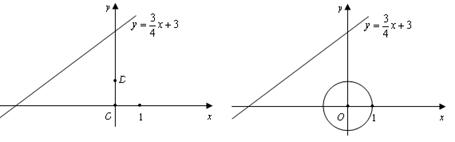
相关知识点
推荐套卷
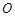 为直线
为直线 上一点,过点
上一点,过点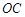 、
、 、
、 , 且
, 且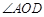 ,
,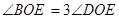 ,
,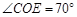 ,求
,求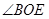 的度数.
的度数.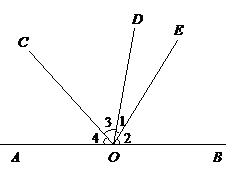
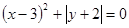 ,求代数式
,求代数式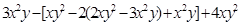 的值.
的值.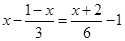
 粤公网安备 44130202000953号
粤公网安备 44130202000953号