高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km—5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内大约有多少千米?( =1.732,
=1.732,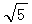 =2.236,结果精确到0.01km.)
=2.236,结果精确到0.01km.)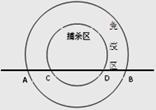
相关知识点
推荐套卷
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km—5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内大约有多少千米?( =1.732,
=1.732,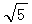 =2.236,结果精确到0.01km.)
=2.236,结果精确到0.01km.)