如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).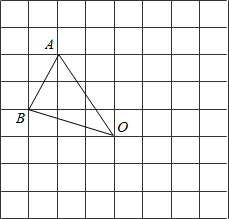
(1)画出△AOB绕点O顺时针旋转90°后的△A1OB1;
(2)请建立直角坐标系并写出点A1的坐标;
(3)求四边形AOA1B1的面积.
相关知识点
推荐套卷
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
(1)画出△AOB绕点O顺时针旋转90°后的△A1OB1;
(2)请建立直角坐标系并写出点A1的坐标;
(3)求四边形AOA1B1的面积.