如图，在平行四边形ABCD中，AD=4cm，∠A=60°，BD⊥AD．一动点P从A出发，以每秒1cm的速度沿A→B→C的路线匀速运动，过点P作直线PM，使PM⊥AD．
（1）当点P运动2秒时，设直线PM与AD相交于点E，求△APE的面积；
（2）当点P运动2秒时，另一动点Q也从A出发沿A→B→C的路线运动，且在AB上以每秒1cm的速度匀速运动，在BC上以每秒2cm的速度匀速运动．过Q作直线QN，使QN∥PM．设点Q运动的时间为t秒（0≤t≤10），直线PM与QN截平行四边形ABCD所得图形的面积为Scm2．
①求S关于t的函数关系式；
②（附加题）求S的最大值．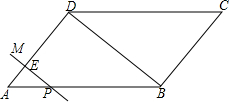
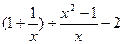相关试题
在国家下身的宏观调控下，某市的商品房成交价由今年3月分的14000元/
下降到5月分的12600元/；
（1）问4、5两月平均每月降价的百分率是多少？（参考数据：
）
（2）如果房价继续回落，按此降价的百分率
，你预测到7月分
该市的商品房成交均价是否会跌破10000元/？请说明理由。
．甲、乙两个同学在
的条件下分别计算了
和
的值．甲说
，其中
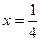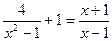
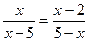
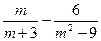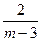
粤公网安备 44130202000953号