(12分)在平面直角坐标系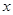 O
O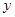 中,直线
中,直线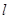 与抛物线
与抛物线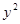 =2
=2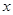 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求证:命题“如果直线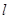 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
相关知识点
推荐套卷
(12分)在平面直角坐标系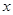 O
O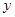 中,直线
中,直线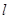 与抛物线
与抛物线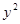 =2
=2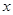 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求证:命题“如果直线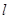 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.