给定下列命题:
①半径为2,圆心角的弧度数为 的扇形的面积为
的扇形的面积为 ;
;
②若 、
、 为锐角,
为锐角, ,
,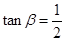 ,则
,则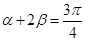 ;
;
③若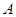 、
、 是△
是△ 的两个内角,且
的两个内角,且 ,则
,则 ;
;
④若 分别是△
分别是△ 的三个内角
的三个内角 所对边的长,
所对边的长,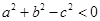 ,则△
,则△ 一定是钝角三角形.
一定是钝角三角形.
其中真命题的序号是 .
相关知识点
推荐套卷
给定下列命题:
①半径为2,圆心角的弧度数为 的扇形的面积为
的扇形的面积为 ;
;
②若 、
、 为锐角,
为锐角, ,
,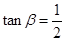 ,则
,则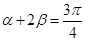 ;
;
③若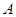 、
、 是△
是△ 的两个内角,且
的两个内角,且 ,则
,则 ;
;
④若 分别是△
分别是△ 的三个内角
的三个内角 所对边的长,
所对边的长,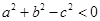 ,则△
,则△ 一定是钝角三角形.
一定是钝角三角形.
其中真命题的序号是 .