两个盒内分别盛着写有0,1,2,3,4,5六个数字的六张卡片,若从每盒中各取一张,求所取两数之和等于6的概率,现有甲、乙两人分别给出的一种解法:
甲的解法:因为两数之和可有0,1,2,…,10共11种不同的结果,所以所求概率为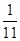 .
.
乙的解法:从每盒中各取一张卡片,共有36种取法,其中和为6的情况有5种:(1,5)、(5,1)、(2,4)、(4,2)、(3,3)因此所求概率为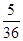 .
.
试问哪一种解法正确?为什么?
推荐套卷
两个盒内分别盛着写有0,1,2,3,4,5六个数字的六张卡片,若从每盒中各取一张,求所取两数之和等于6的概率,现有甲、乙两人分别给出的一种解法:
甲的解法:因为两数之和可有0,1,2,…,10共11种不同的结果,所以所求概率为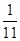 .
.
乙的解法:从每盒中各取一张卡片,共有36种取法,其中和为6的情况有5种:(1,5)、(5,1)、(2,4)、(4,2)、(3,3)因此所求概率为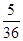 .
.
试问哪一种解法正确?为什么?