（本小题满分12分）
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇.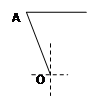
(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行时间应为多少小时？
(Ⅱ)为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值；
.
，求
的极值；
的取值范围.
.
的最小正周期；
在
处取得最大值，求
的值;
的单调递增区间.
为等差数列，且
.
项和
；
满足
求数列
的角
的对边分别为
，已知
.
；
，
,求
的值.
；
.推荐套卷
（本小题满分12分）
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇.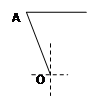
(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行时间应为多少小时？
(Ⅱ)为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值；
粤公网安备 44130202000953号