中国象棋棋盘中蕴含着平面直角坐标系，如图9是中国象棋棋盘的一半，棋子“马”走的规则是沿“日”形的对角线走. 例如：图中“马”所在的位置可以直接走到点A、B处.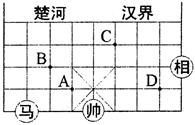
(1)如果“帅”位于点 (0，0)，“相”位于点(4，2)，则“马”所在的点的坐标为 ，点C的坐标为 ，点D的坐标为 .
(2)若“马”的位置在C点，为了到达D点，请按“马”走的规则，在图中画出一种你认为合理的行走路线，并用坐标表示.
相关试题
小军的爸爸早晨从家骑自行车送小军去学校上学，他们的速度是12千米/时，用了0.5小时到达学校；放学时，让小军坐汽车，汽车的速度为V千米/时．
（1）写出t与V之间的函数关系式；
（2）如果小军要在10分钟内回到家，那么汽车的速度至少为多少？
某工厂承担了加工2100个机器零件的任务，甲车间单独加工了900个零件后，由于任务紧急，要求乙车间与甲车间同时加工，结果比原计划提前12天完成任务，已知乙车间的工作效率是甲车间的1.5倍。求甲、乙两车间每天加工零件各多少件？
＝
粤公网安备 44130202000953号