在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(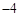 ,5),(
,5),( ,3).
,3).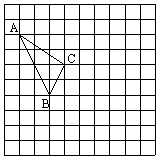
⑴请在如图所示的网格内作出x轴、y轴;
⑵请作出将△ABC向下平移的3个单位,向右平移2个单位后的△A′B′C′;
⑶写出点B′的坐标并求出△ABC的面积.
相关知识点
推荐套卷
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(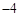 ,5),(
,5),( ,3).
,3).
⑴请在如图所示的网格内作出x轴、y轴;
⑵请作出将△ABC向下平移的3个单位,向右平移2个单位后的△A′B′C′;
⑶写出点B′的坐标并求出△ABC的面积.