根据下面给出的数轴,解答下面的问题: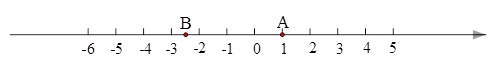
⑴ 请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: B: ;
⑵ 观察数轴,与点A的距离为4的点表示的数是: ;
⑶ 若将数轴折叠,使得A点与-2表示的点重合,则B点与数 表示的点重合;
⑷ 若数轴上M、N两点之间的距离为2010(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
相关知识点
推荐套卷
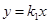 的图象于反比例函数
的图象于反比例函数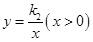 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.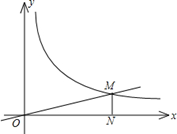
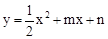 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.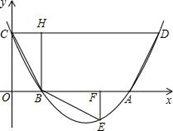
 ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.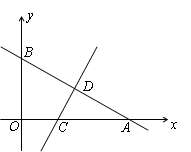
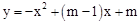 与y轴交于点(0,3).
与y轴交于点(0,3). 粤公网安备 44130202000953号
粤公网安备 44130202000953号