（理）已知数列{an}的前n项和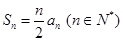
，且
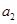=1，
.
（I）求数列{an}的通项公式；
（II）已知定理：“若函数f(x)在区间D上是凹函数，x>y(x,y∈D)，且f’(x)存在，则有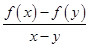
< f’(x)”．若且函数y=xn+1在(0,+∞)上是凹函数，试判断bn与bn+1的大小；
（III）求证：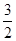
≤bn<2.
相关试题
是分别从集合A={1，2，3，4}中随机抽取的元素，集合B=
的所有实数对
与
的值满足
的概率.
的函数
是奇函数
的解析式；
，不等式
恒成立，求
的取值范围.
为偶函数，且在区间
上是单调递减函数，
的解析式；
的奇偶性。
，求
的值；
，
，求
的范围.
，且满足
的值；
，
，求
的值。推荐套卷
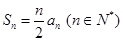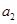（理）已知数列{an}的前n项和，且=1，.
（I）求数列{an}的通项公式；
（II）已知定理：“若函数f(x)在区间D上是凹函数，x>y(x,y∈D)，且f’(x)存在，则有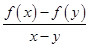
< f’(x)”．若且函数y=xn+1在(0,+∞)上是凹函数，试判断bn与bn+1的大小；
（III）求证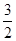：≤bn<2.
粤公网安备 44130202000953号