（理）如图，|AB|=2，O为AB中点，直线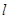
过B且垂直于AB，过A的动直线与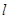交于点C，点M在线段AC上，满足
=
.
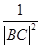（1）求点M的轨迹方程；
（2）若过B点且斜率为-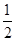 
的直线与轨迹M交于点P，点Q(t,0)是x轴上任意一点，求当ΔBPQ为锐角三角形时t的取值范围．
，解不等式
；
求a的取值范围.
，求x为何值时
有最大值，最大值
的极大值。
，命题q：
，若
与
都为假命题，求x的值。
,
是平面上一动点,且满足
,
对应的方程;
在曲线
作曲线
,且
满足
,试判断动直线
是否过定点,并证明你的结论.推荐套卷
（理）如图，|AB|=2，O为AB中点，直线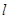过B且垂直于AB，过A的动直线与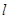交于点C，点M在线段AC上，满足=.
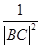（1）求点M的轨迹方程；
（2）若过B点且斜率为- 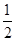的直线与轨迹M交于点P，点Q(t,0)是x轴上任意一点，求当ΔBPQ为锐角三角形时t的取值范围．
粤公网安备 44130202000953号