如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.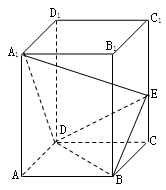
(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离
推荐套卷
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离