(I) 已知抛物线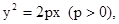 过焦点
过焦点 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;
(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点 的动直线 l 交抛物线于
的动直线 l 交抛物线于 两点, 存在定点
两点, 存在定点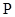 , 使得
, 使得 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.
相关知识点
推荐套卷
(I) 已知抛物线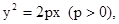 过焦点
过焦点 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;
(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点 的动直线 l 交抛物线于
的动直线 l 交抛物线于 两点, 存在定点
两点, 存在定点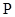 , 使得
, 使得 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.