已知一元二次方程 中,如果
中,如果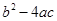 ≥
≥ ,那么它的两个实数根是
,那么它的两个实数根是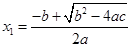 ,
,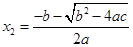 .
.
(1)计算: 、
、 的值(用含
的值(用含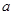 、
、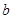 、
、 的代数式表示);
的代数式表示);
(2)设方程 的两个根分别为
的两个根分别为 、
、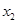 ,根据(1)所求的结果,不解方程,直接写出
,根据(1)所求的结果,不解方程,直接写出 = ,
= , = ;
= ;
(3)如果方程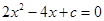 的一根是
的一根是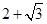 ,请你利用(1)中根与系数的关系求出方程的另一根及
,请你利用(1)中根与系数的关系求出方程的另一根及 的值.
的值.
相关知识点
推荐套卷
已知一元二次方程 中,如果
中,如果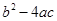 ≥
≥ ,那么它的两个实数根是
,那么它的两个实数根是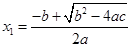 ,
,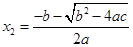 .
.
(1)计算: 、
、 的值(用含
的值(用含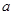 、
、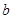 、
、 的代数式表示);
的代数式表示);
(2)设方程 的两个根分别为
的两个根分别为 、
、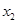 ,根据(1)所求的结果,不解方程,直接写出
,根据(1)所求的结果,不解方程,直接写出 = ,
= , = ;
= ;
(3)如果方程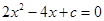 的一根是
的一根是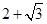 ,请你利用(1)中根与系数的关系求出方程的另一根及
,请你利用(1)中根与系数的关系求出方程的另一根及 的值.
的值.