(本小题满分14分) 如图，已知抛物线与坐标轴分别交于A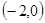
、B
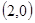、C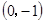
三点，过坐标原点O的直线
与抛物线交于M、N两点.分别过点C、D
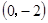作平行于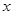
轴的直线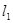
、
.（1）求抛物线对应的二次函数的解析式；（2）求证:以ON为直径的圆与直线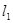相切；（3）求线段MN的长（用
表示），并证明M、N两点到直线的距离之和等于线段MN的长.
推荐套卷
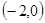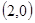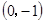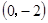(本小题满分14分) 如图，已知抛物线与坐标轴分别交于A、B、C三点，过坐标原点O的直线与抛物线交于M、N两点.分别过点C、D作平行于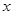轴的直线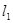、.（1）求抛物线对应的二次函数的解析式；（2）求证:以ON为直径的圆与直线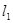相切；（3）求线段MN的长（用表示），并证明M、N两点到直线的距离之和等于线段MN的长.
粤公网安备 44130202000953号