如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=" 17," 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.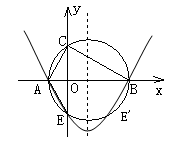
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
相关试题
有一些分别标有3，6，9，12。。。。的卡片，后一张卡片上的数比前一张卡片上的数大3，小华拿到了相邻的5张卡片，这些卡片之和为150。
（1）小华拿到了哪5张卡片？
（2）你能拿到5张相邻卡片，使得这些卡片上的数之和为100吗？
下表为某月的月历。
| 日 |
一 |
二 |
三 |
四 |
五 |
六 |
| 1 |
2 |
3 |
4 |
5 |
||
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 20 |
21 |
22 |
23 |
24 |
25 |
26 |
| 27 |
28 |
29 |
30 |
31 |
（1）在此月历上用一个矩形任意圈出2
3个数，如果圈出的6个数之和为51，这6天分别是几号？
（2）观察此月历，你还能提出其他的问题吗？
粤公网安备 44130202000953号