如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.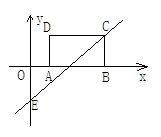
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.
相关试题
如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.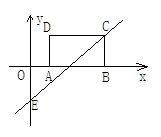
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.
的方程
.
，求另一个根及
值.
时，有一位同学解答如下：
， 
，
粤公网安备 44130202000953号