(本小题满分1 3分)
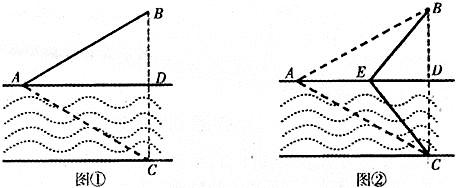
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE="θ" (0≤θ≤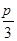 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.